Tackling a medium-difficulty challenge
In my previous post, I took up the challenge of completing a leetcode.com problem to prove that low-code is more than just a one-form solution – it’s got the flexibility needed to take on even the more difficult technical problems. The one I chose was Two Sum, the first challenge on the site and one of the “easy” challenges (you can read all about it here).
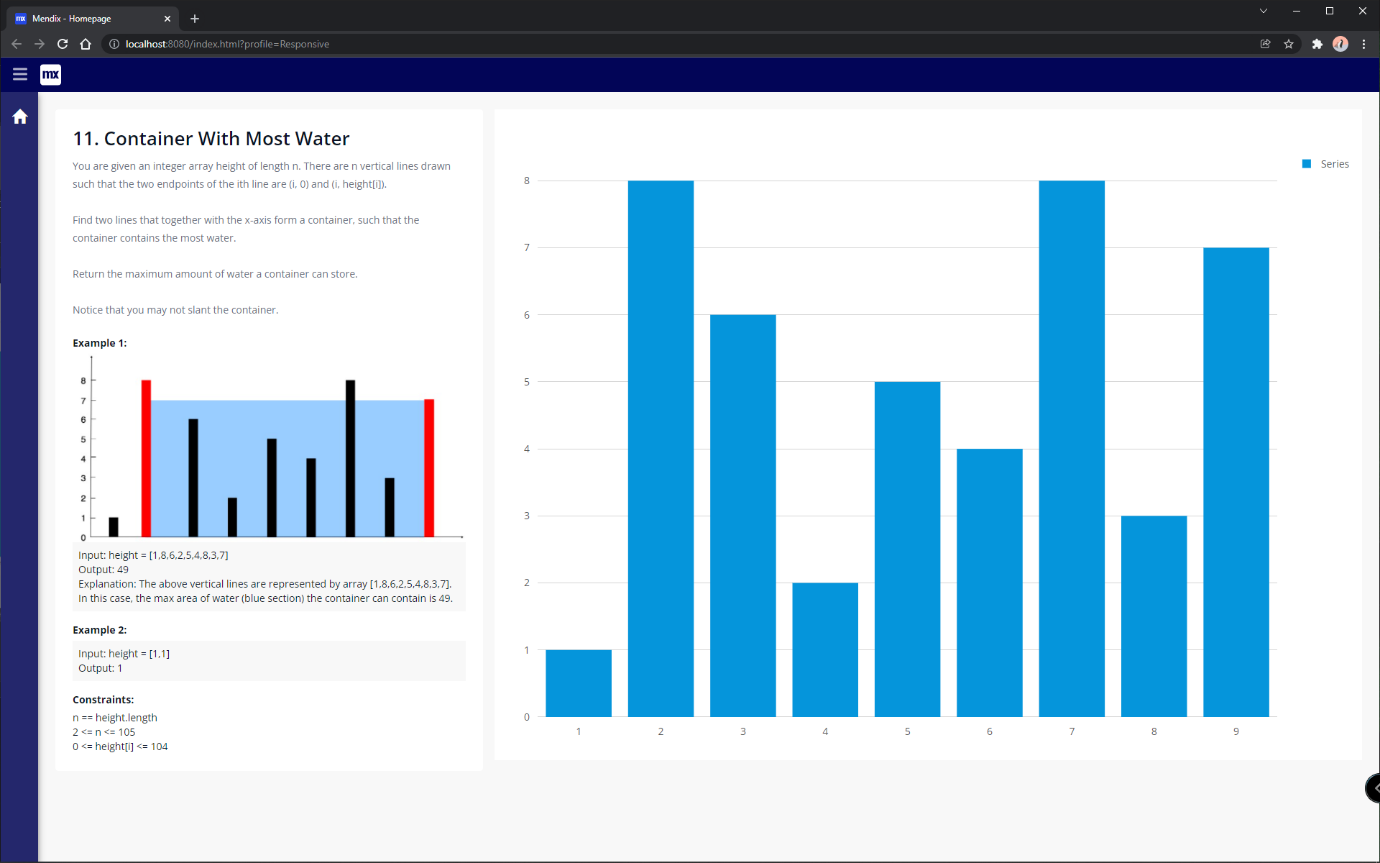
This time around I’m going to tackle something a bit trickier: Challenge eleven – “Container With Most Water” – a medium difficulty challenge. This problem involves taking an array of column heights and working out which pair of columns form a container that could hold the most water; or has the biggest rectangular area between them.
“Container With Most Water” – Where to begin
In the last challenge we started from a point of accepting the challenge at face value and approaching it on a level playing field, using as basic an approach as possible, and then leaning into how it should be done in low-code. We’re going to skip that this time and get straight to tackling this problem in low-code.
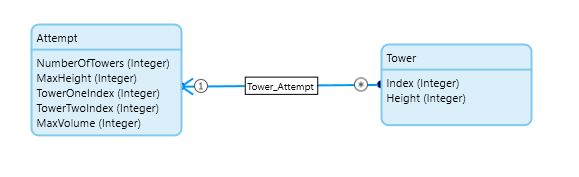
First up, we need some data. We’re going to create an entity to store our result in and a child entity to create the “tower” data in:
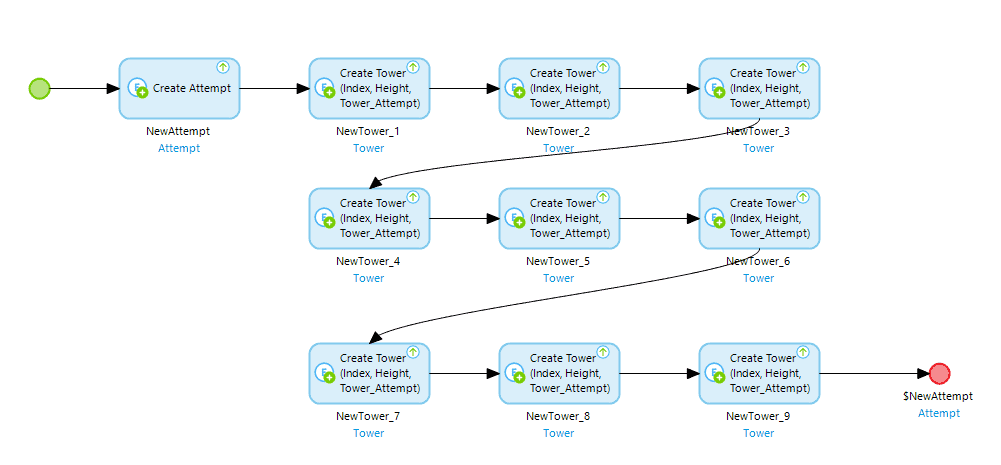
This will give us a space to randomly generate a series of values and place them in a set order and somewhere to group them together to store the results of our attempts. Before we randomly generate a dataset though, it would serve us best to create a list of values based on the example. Doing this in low-code isn’t particularly elegant but it is straightforward: We simply create each item one at a time, link it to the attempt and return our “Attempt” entity.
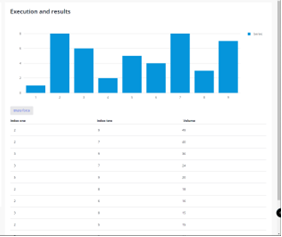
It’s not pretty but it gets us where we need to be. The chart on the right is rendered from the data we’ve just created.
First attempt – brute force
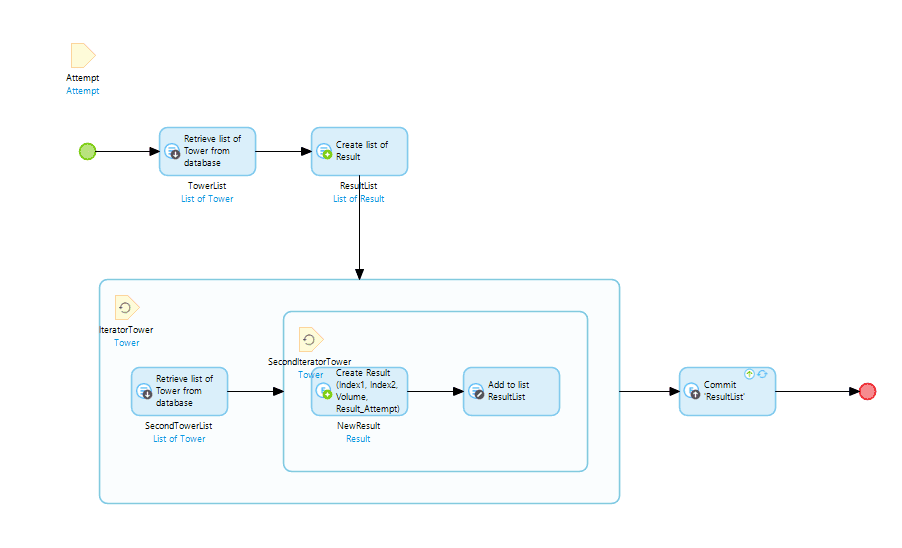
We’ll start basic with a brute force attempt. We can be sure that this isn’t going to be the best solution but it’s always worth doing to find the correct answer for a given array so that we can check our answer when we move on to a more efficient version. To do this, we’ll go with a nested loop: The first loop goes through all the Towers, and the second every Tower that follows the current iterator in the outer loop.
As you can see from the Microflow it’s an O(n2) efficiency, not great, but let’s check it comes up with the right answer.
As we can see from the results table, we’ve managed to reach the right conclusion. That’s great. The next step let’s see if we can do it in a more efficient way.
Next attempt – let’s go for efficiency
To do that, we’ll need to work out what the best quickest way is to find that container and, much like the last example we did, it’s to use pointers.
We’ll start at both ends and move inwards keeping the tallest Tower from the pair and moving the other pointer. We’ll need to check each volume and keep a log so we can then sort it to find the biggest volume. By iterating this way we’re moving from checking the largest width to the largest height and we’re checking all the best combinations for calculating the volume.
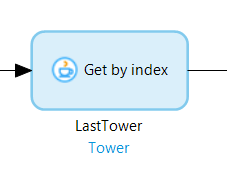
To do this we’re going to address a shortcoming in the last exercise. Mendix, by default, doesn’t allow for retrieving an element of an in-memory list by its index. You can easily do it when pulling from the database but that wouldn’t be very efficient. To correct this, we can create a simple Java action:
Extending functionality in Mendix with Java actions
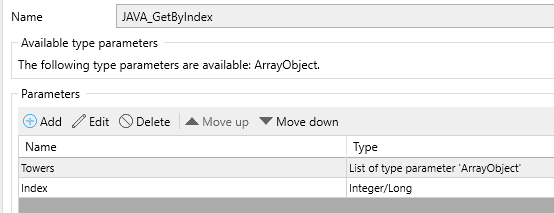
One of the real plus points for Mendix is that you’re not limited by the platform to only the tools in the toolbox. You can quickly and easily extend functionality by either grabbing something from the marketplace or creating your own custom Java action! In our case, it’s quite a simple ask to make this function, pass in a list, then an index, and then return the appropriate object.
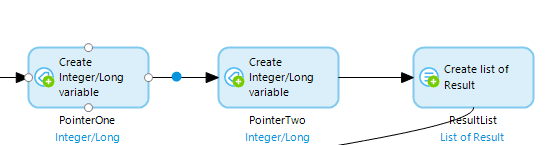
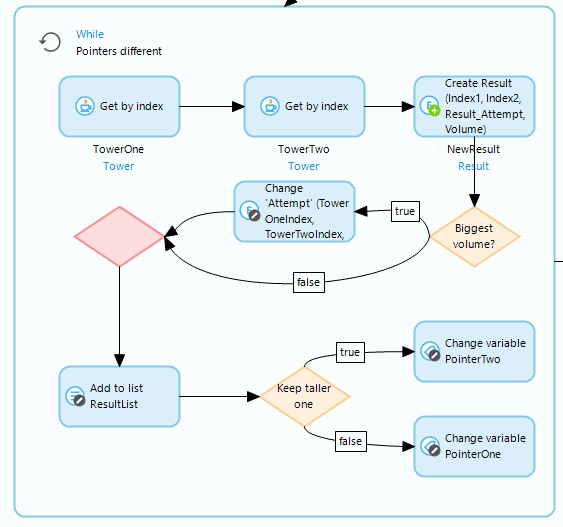
Now we can use pointers the way you would in most programming languages when accessing lists. For the efficient pass, we’re going to need two integer pointers, to keep track of our checks from both ends, and a list to put our results in.
Then we’re going to start a While loop and we’ll keep iterating until both our pointers meet at a single Tower, at which point we’ll know to stop. Inside this loop we’ll get the Tower for each pointer and calculate the volume that could be contained between the Towers. As we loop through, we’ll also keep track of the biggest volume we’ve found in the attributes we added earlier in the Attempt entity. This way we’ll know what the largest volume is, and which two Towers create that volume.
Before we end the loop iteration and move onto the next, we’ll check which of the two Towers we’ve just compared is taller. If it’s Tower one then we’ll reduce pointer two, if it’s Tower two then we’ll increase pointer one. This brings in the pointers until they meet at the same Tower and satisfy our While loops escape clause. All that looks like this…
The results of the efficiency attempts
A couple of commits at the end to track our attempts and we are done. We can then execute the new process and see the results:
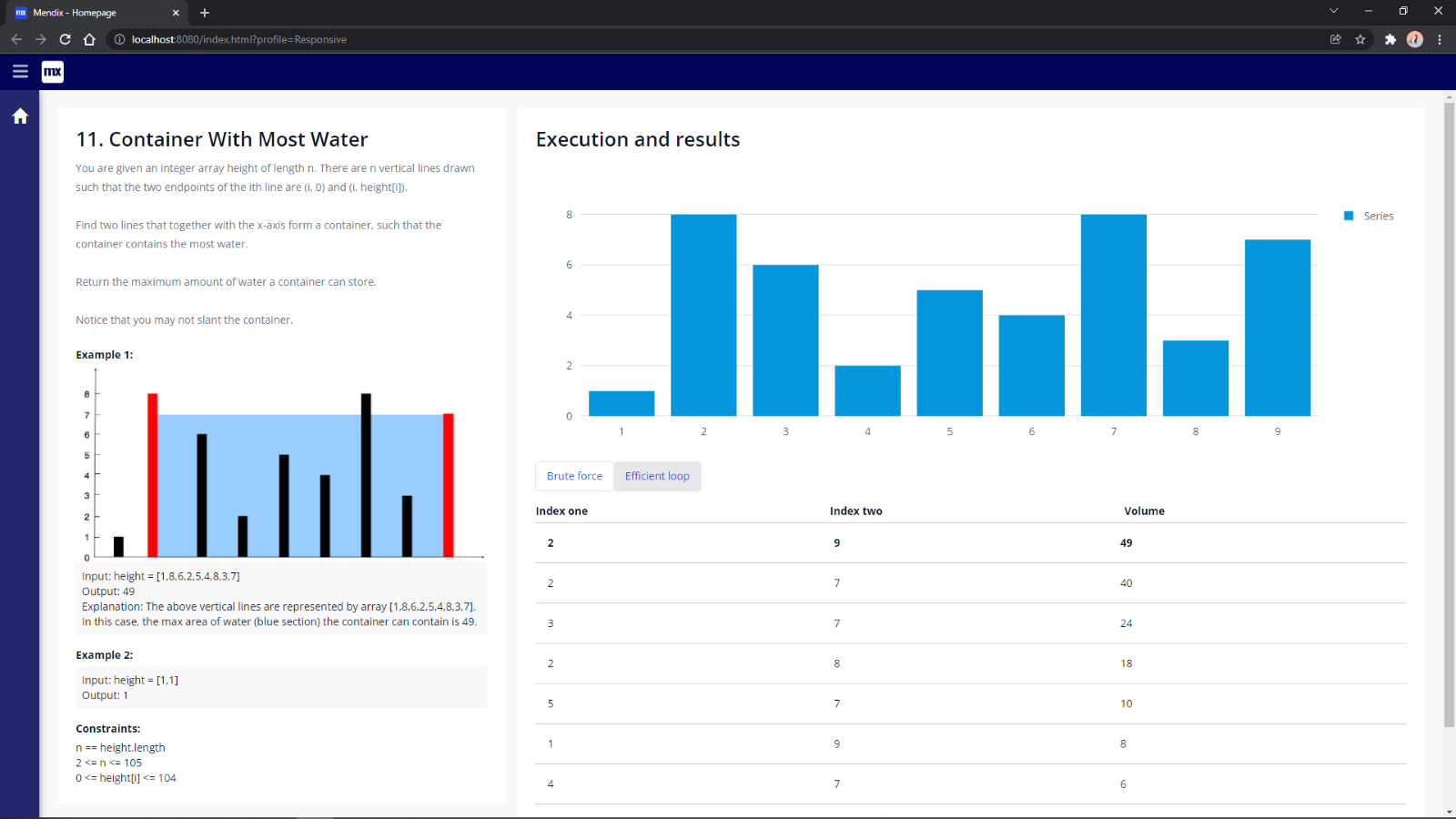
Here we can see we’ve reached the right conclusion in only six attempts rather than the thirty-six attempts it took with the brute force approach. This means another challenge successfully completed in low-code, with the addition of a small amount of code just to make life a bit easier.